- Which factor does not impact the complexity of an incident?: Assignment, uk
- You are applying for a job as a junior in-house lawyer at a fashion house. To evaluate your expertise: Consumer and Intellectual Property law Assignment, UOL, UK
- QSP7BEC: Explains the need to update the cost advice from 2019 identifying reasons with examples: Building Economics Assignment, UCEM, UK
- Identify how you have applied OB theory, learned during the module and to develop your knowledge: Organisational behaviour Assignment, OU, UK
- COMP6029: Computer Science and Electronic Engineering related subjects generally use the IEEE referencing style: Network Systems Course Work, UOS, UK
- Describe internal governance procedures used within own organisation: Leadership and Management for Adult Care Assignment, CIPD, UK
- Select an organization of choice but of Pakistan’s origin. The size of selected organization: 30 Resource And Talent Planning (Level 5) Assignment, OU, UK
- You are required to undertake an empirical project involving the analysis: The Social protection Survey Assignment, UOS, UK
- Explain what is meant by restrictive practices, restraint, deprivation of liberty LZ, best-interest decisions: Healthcare Assignment, BCU, UK
- Identify the key provisions of legislation, codes of practice and policies regarding mental: Healthcare Assignment, BCU, UK
- Review the benefits of coaching and mentoring relationships to both parties: Leadership and Management Assignment, UL, UK
- Analyze the difference between coaching and mentoring, giving examples of how each process: Leadership and Management Assignment, UL, UK
- Evaluate ways to address challenges arising during professional supervision: Leadership and Management Assignment, UL, UK
- Analyse factors that can result in a power imbalance in professional supervision and how to address them: Leadership and Management Assignment, UL, UK
- Evaluate how supervision can be used alongside appraisal and professional development processes: Leadership and Management Assignment, UL, UK
- Describe how external and internal factors influence practice and can be used within professional supervision objectives: Leadership and Management Assignment, UL, UK
- Explain why the well-being of the supervisee should be included within effective supervision: Leadership and Management Assignment, UL, UK
- Analyze how effective supervision can protect the supervisor and the organization: Leadership and Management Assignment, UL, UK
- Analyze how effective supervision should be used to support and protect: • the supervisee: Leadership and Management Assignment, UL, UK
- Compare different supervision activities and processes which can be used in adult care: Leadership and Management Assignment, UL, UK
MAST4001: Explain two different methods to solve a quadratic equation and what is meant by a real root: Algebraic Methods Assignment, UOK, UK
| University | University of kent (UOK) |
| Subject | MAST4001: Algebraic Methods |
Questions
a) Explain two different methods to solve a quadratic equation and what is meant by a real root. For each, describe an instance where it would be appropriate to use this method and give an example calculation.
b) Define the discriminant (sometimes known as determinant) of a quadratic equation and, using your own words, explain how it can be used to determine the number of solutions to the equation. Show example calculations to where one, two, or no real roots are found. Use hand-drawn or software-generated graphs to show the roots of the quadratic and indicate which roots are real.
c) Explain in your own words how to determine whether a geometric series will:
- converge
- diverge
- oscillate Define any algebraic variables you use.
d) Give an example of each type of series and carry out an example calculation to show that it converges, diverges, or oscillates.
You can either print out the document and answer on the sheet, or answer on separate paper. Once you’ve finished, either scan or clearly photograph your answers to upload them to your assignment.
1
2
a) Express x² + 4x – 7 in the form (x + p)² – q, where p and q are integers.
b) Hence, or otherwise, find the coordinates of the minimum point of the curve y = x² + 4x – 7.
3. The quadratic equation x² + (3k + 1)x + (4 – 9k), where k is constant, has repeated roots.
a) Show that 9k² + 42k – 15 = 0.
b) Hence find the possible values of k.
4.
a) Find the binomial expansion of (2 + 3x)5, simplifying the terms.
b) Hence find the binomial expansion of (2 + 3x)5 – (2 – 3x)5
5.
a) Evaluate and simplify the following logarithm to find x 2logb 5 + ½ log 9 − log 3 = logo x
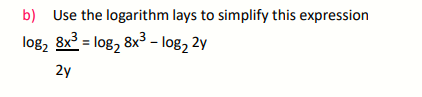
c) The formula for the amount of energy E (in joules) released by an earthquake is E = (1.74 × 1019 × 101.44M) where M is the magnitude of the earthquake on the Richter scale.
i. The Newcastle earthquake in 1989 had a magnitude of 5 on the Richter scale. How many joules were released?
ii. In an earthquake in San Francisco in the 1900s the amount of energy released was double that of the Newcastle earthquake. What was its Richter magnitude?
6.
The first term of an infinite geometric series is 96. The common ratio of the series is 0.4.
a) Find the third term of the series.
b) Find the sum to infinity of the series.
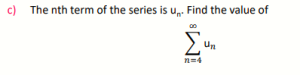
7.
An arithmetic series has first term a and common difference d. The sum of the first ten terms of the series is 460.
a) Show that 2a + 9d = 92.
b) Given also that the 25th term of the sequence is 241, find the value of d.
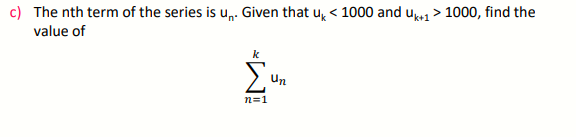
Buy Answer of This Assessment & Raise Your Grades
Students Assignment Help UK offers the best Online Assignment Help to college students who wish to score top grades in their MAST4001: Algebraic Methods assignment. Our team of subject-oriented and highly qualified writers promises to deliver the best quality solution on engineering assignments at a discounted price.
Answer
