- LAW6006: Critically analyze the role and nature of the employment tribunal Is the current structure effective: Employment Law Assignment, AU, UK
- 5CO03: You have been asked by your CIPD Branch to lead a discussion at one of its events: Professional Behaviors And Valuing People Assignment, UOL, UK
- LART 1001: Is it possible to isolate from globalization and Why and why not Challenges and opportunities of Globalization: Introduction to Civics and Ethics Assignment, ASTU, UK
- MATHS4102: Effective heat transfer is essential for energy systems. In a smooth channel, heat transfer is achieved by forced convection: Fluid Mechanics Assignment, UOG, UK
- 6008LBSBSC: UK Oil Plc is involved in upstream, oil exploration and production in the North Sea, United Kingdom: Strategic Corporate and Project Finance Assignment, LJMU, UK
- MAST4001: Explain two different methods to solve a quadratic equation and what is meant by a real root: Algebraic Methods Assignment, UOK, UK
- Explain any 2 Covid 19 organizational challenges and their possible solutions: Human Resources Management Assignment, QUB, UK
- Explain the importance of a holistic approach to assessment and planning of care or support: Level 3 Diploma in Adult Care Assignment, CRC, UK
- Different ideologies of education lead to different ways of looking at the curriculum, or curriculum: Developing Professional Practice Assignment, UOE, UK
- Produce a display or booklet for your setting that gives clear information on the ages and stages of a child’s development: Children’s Learning and Development Assignment, EHU, UK
- You work as a Test Engineer for a global manufacturer of electrical and mechanical components and systems: Mathematics Assignment, NUN, UK
- MT1174: You are working as a Junior Engineer for a small motor racing team and You have been given a proposed mathematical: Calculus Assignment, UOL, UK
- You are working as a tax senior in Jhon& Smith tax consultants and You have just earned your new role of tax: Taxation Assignment, OU, UK
- You will demonstrate independent thinking relating to individual case management and preparation of the perioperative environment: Storyboards Assignment, LAU, UK
- Identify an appropriate theme and title for a research project and Develop and justify a research hypothesis using relevant literature: Healthcare science Assignment, MUL, UK
- Using the role, you have decided upon for your future career, write an information sheet for someone who is considering studying: Health and Social Care Assignment, LMU, UK
- LAWS2029: Discuss the purpose of employment regulation and the way that it is enforced in practice: Foundations in Criminal Evidence Law Assignment, UOS, UK
- LAWS2029: Explain how the legal and evidential burdens will apply to the prosecution of Dean for the murder: Foundations in Criminal Evidence Law Assignment, UOS, UK
- Explain how your research fits into existing published work and Do this by locating and critically reviewing about 10-12 sources: Research Methods Assignment, UON, UK
- You work as a digital marketing analyst, for Cambridge Digital, a marketing consultancy company: Master of Digital Marketing Assignment, UOM, UK
NHA2414: Draw a free body diagram (FBD) and derive the equation of motion of m with y(t) as the input, and obtain the transfer function: Dynamic Analysis and Control Assignment, UOH, UK
| University | University of Huddersfield (UOH) |
| Subject | NHA2414: Dynamic Analysis and Control |
Task 1
The quarter-car model of a vehicle suspension and its free body diagram is shown in Figure 1. In this simplified model, the masses of the wheel, tire, and axle are neglected, and the mass m represents one-fourth of the vehicle mass. The spring constant k models the elasticity of both the tire and the suspension spring. The damping constant c models the shock absorber. The equilibrium position of m when y=0 is x=0. The road surface displacement y(t) can be derived from the road surface profile and the car’s speed.
- Draw a free body diagram (FBD) and derive the equation of motion of m with y(t) as the input, and obtain the transfer function.
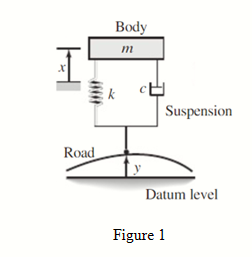
If assume:
m=250 kg
k=10000, 30000, 50000 N/m
c=1000, 2000, 3000 N.s/m
- Plot magnification ratio vs frequency ratio (r=0-4) diagrams for the parameters given above (you can draw the three curves in one diagram for three different k values and do the same for the three c values as well).
- Use the derived transfer function to model the system and plot the step response for the system by Matlab or Simulink.
Task 2
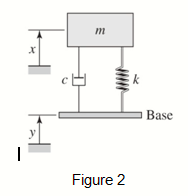
A common example of base excitation is caused by a vehicle moving along a bumpy road surface as shown in Figure 2. This motion produces a displacement input to the suspension system via the wheels. The second task is to calculate and draw a displacement transmissibility ratio diagram for a quarter car with 250 kg, the spring constant is 10000 N/m, but varying damping constant to be 1000, 2000, 3000, 5000, and 10000 N.s/m. If the vehicle driver wishes to reduce the vehicle’s body displacement, what suggestion you could make for the driver and why?
Are You Looking for Answer of This Assignment or Essay
Do you need help with NHA2414: Dynamic Analysis and Control assignments? Don’t look further and take our pay for college assignments service at Students Assignment Help UK. our executives are available 24*7 hours to provide appropriate solutions on engineering assignments at a market price.
Answer
